In brief (in a journal paper, this would be the 'abstract'):
- You need 20-30 years of data to define a climate trend in global mean temperature
- Forward and backward trends are markedly different
- Therefore, to discuss climate trends in global mean temperature, you need to use 20-30 years of data centered on the date of interest.
Let's consider the first point -- how long it takes to determine a climate trend in global mean temperature. We could define a trend with 2 minutes of data -- temperature at one minute, temperature at the next minute, and draw a straight line through the two numbers. We'd wind up with wildly varying trends, though, from minute to minute through the year. This is weather and turbulence. Make it daily or monthly averages, and we still have the wildly varying trends, and the magnitude of those trends will depend on what time period we chose. Rather than declare that 'this is the right period', we'll determine it by looking at the data itself.
If it is meaningful to talk about climate as opposed to weather, there has to be a time span over which our result for describing climate does not depend much on how long a time span we choose. For average climate temperature, we found 20-30 years as the appropriate time span. I didn't show the figures then, but it's in the program and output you can pick up from my web site that this is also the appropriate time span for deciding a climate temperature variance (how much scatter there is about the average; even if the average didn't change, we would probably consider it a climate change to have winter lows vary from -30 to +15 instead of -10 to -5).
Figure 1 here shows the trends for all years (remember I'm lopping off the first 31 and last 31 from the NCDC record) that I computed trends for, by all 3 methods, in terms of the length of data record used. So at 36 (months) we see a range in the computed trends between +15 C/century and -15 C/century. These are enormous values cmpared to what we think of for climate change. If I wanted to give you a wrong impression about climate, then, I could use such short records. The range declines as we take longer periods. And then flattens out for trend periods of 252-372 months (21-31 years -- remember I took only odd averaging periods). In this part of the display, the range is about +1.5 C/century to -1.5 C/century -- and it is independant of how long an average I took. This, then, supports that a) there is such a thing as a climate temperature trend and b) that you need 21-31 years to find it (we can round to 20-30, given how 19 years is close to 21 also, we expect 20 even to be so as well).
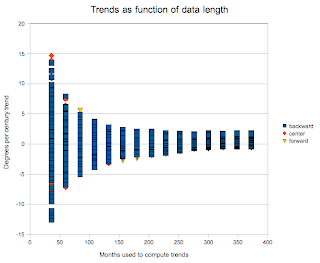
Statistical aside: To compute variance, we find the deviation of each observation from the mean, square it, and then add this value up for all observations and divide by the number of observations. (Or use the appropriate function in your spreadsheet.) This is a fundamentally meaningful quantity. If we then take the square root of this number, and the numbers have a normal distribution, then we have a standard deviation. We can always take the square root of the variance, but it will not always be a standard deviation.
In figure 2, I plot instead the maximum and minumum trends, and the square root of variance -- again in terms of how long a period is used to compute the trends. This shows fundamentally the same information, but perhaps a little more clearly. Aside: It's a good idea to look at your data from several different vantages. Sometimes the display method you use in one step can hide something that's blindingly obvious in another method. Again, we see that the figures (maximum trend, minimum trend, average trend, square root of variance in trend) all stabilize once the data length used is 20-30 years. And, conversely, that for periods of 3-13 years, the figures all depend sensitively on how long an averaging period you choose.

Choose is a key word in doing science. We try to avoid having choices. Choices can be made differently by different people, for different reasons, and not all those reasons will turn out to be good ones. Finding a scientific principle and then looking for how to satisfy that principle is far better. Here, the principle is that the length of data used should not affect your conclusion about what the climate trend is. This is a strong principle. So when you see someone violating it (say by using a 7 year span without doing some real work to justify it -- work like I'm doing here), they're probably not doing good science.
Now, in figure 3, let's look at what the trends are like if we use 7 years of data, versus using 25 years. I'm computing all these by using centered information -- data evenly on either side of the time of interest. We'll get to why this is best in a minute. The main thing I think this shows is that if you use the short period, you present a false impression that climate is highly variable, trends changing from some very high positive value to a high negative value in a span not terribly longer than the 7 years' data you used in either case. This makes no sense for climate, but does for weather, or for misleading people. Weather, we know, does change rapidly. We can be warmer than usual for a few days (or months, or years) and then cool a few days/months/years later. Nobody (scientific) has ever said weather was going to end. Go out to the 25 year data period trends and we see, instead, that the trends have more stable behavior. They do change, which is reasonable since we do expect that climate changes. But it's no longer large magnitude flip-flops. That, too, makes sense as climate is a big beast and turning on a dime has to be a rare if ever occurrence.

To look a little differently at it ... if someone shows you a trend over 3 years, about 90% of what they're showing you is weather (real trends of up to 1.5 C/century, 3 year trends of up to 15 C/century -- 90% of that 15 C/century is weather). For a 7 year trend, it's about 70% weather. Weather is interesting, but if you're interested in climate, and they're claiming to be talking about climate, then they're misleading you by those 70-90% of weather they've thrown in by using such short spans.
On to which data to use for computing trends (or, for that matter, averages, but I'm focusing on trends today). Figure 4 shows trends in degrees per century as computed with data forward from the date given, backwards from the date given, and centered on the date shown. It also shows, and this is why I went to degrees per decade -- the magnitudes come out comparable, the NCDC monthly anomalies. I computed the trends using 25 years of data (300 months).
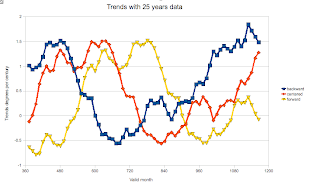
We immediately see that, indeed, the forward and backward trends are quite different, as expected in the planning note 'deciding climate trends'. The curves themselves are actually the same -- but shifted by 25 years (the period used to compute the trend -- when I use 31 years, it's shifted by 31 years, and so on). The centered trends show, again, the same behavior, but now 12.5 years (half my data period) off from the forward, or backward trends. So, look at the data for anomalies versus the different trends as computed. If we look at, say, 1945 (month 780) -- a generally warm year, we see a modestly negative trend from the centered trends, an extremely negative trend if we look forward, and extremely positive if we look backward. What's happening? And which makes most sense for thinking about the 1945 climate trend?
Climate is about normal, our expectations. For 1945, then, would we describe the typical change as one of rapid warming? rapid cooling? a modest cooling? If we look around then, the best description of the tendency is that there's a modest cooling going on. 1930s were warm, 1945 was a particularly warm year, but going in to the 1950s, temperatures were cooler. The large trends, in opposite directions, the forward and backward trend computations give us, even though for an appropriate period, mislead us. The centered trend computation gives us the right idea of what is going on around 1945. Repeat this inspection for other years, and think you'll rapidly come to the conclusion that the best description of what is going on around any given time is the one from a centered computation. If a trend is downwards (negative numbers), then we expect that times before our year of interest are generally warmer than later times. If it's upwards (positive trend), the we expect later years to be warmer. Only the centered computation consistently gives us this result.
We now have 2 conclusions: trends should be computed with 20-30 years of data, and they should be centered on the date of interest. Let's see how it works, applied to as much data as possible. To cover the greatest time span possible, I'll take the shortest data length reasonable for computing trends -- 20 years. Since I'm doing centered computations, this lets me get to within 10 years of the start and end of the record (remember I had been skipping the first and last 31 years so that all three methods could be used, and because I didn't know if some number shorter than 31 years would be long enough). Figure 5 gives the result, in degrees per decade, and with the NCDC monthly anomalies as well.

The most recent year we can compute a good quality trend for is 1998. The trend then is a warming of 0.19 degrees per decade, 1.9 per century. We see that the trend is higher towards the end of the record (i.e., towards the present) than at other times, though we'd have to do additional work to decide whether the difference was physically meaningful. The thing which surprised me about the curve is that most of the time -- from 1890 to 1998 that we can compute a quality trend for -- the climate trend has been a warming. Not a matter of sometimes up, sometimes down, but rather a basically up except for a bit of down in mid-20th century. 70% of the time, we've been seeing warming.
By way of summary, or postscript, or some such ...
- Whether it is to compute the average climate temperature, the variance of climate temperature, or the trends in climate temperature, we need 20-30 years of data.
- On the other hand, it is possible to compute a climate with 20-30 years of data. This didn't have to be the case. I'll show in a later post a curve with no climate in the sense I've been talking about.
- Most of the time for the period of data, we've been experiencing a climate warming.
Update 13 February 2010: The data file I worked on and the program I used are in a tar file. You'll need a fortran compiler for this, or translate it to a language of your choice. Nothing very fortran-ish is being done and the program is short.



26 comments:
Bob, over a year you have a change, not a trend
http://stats.oecd.org/glossary/detail.asp?ID=2769
Definition:
A long-term movement in an ordered series, say a time series, which may be regarded, together with the oscillation and random component, as generating the observed values.
Context:
In time series analysis, a given time series can be decomposed into: a) a cyclical component; b) a trend component; c) a seasonal component; d) an irregular component.
Source Publication:
The International Statistical Institute, “The Oxford Dictionary of Statistical Terms”, edited by Yadolah Dodge, Oxford University Press, 2003.
Isn't it possible, though, to label a particularly large change (e.g. the record Arctic melt in 2007) as significant even when it's too early to calculate a 20-year trend around the year? It should be possible to identify a "weather" element as a leading indicator of a "climate" change by comparing it to the variance over some sufficiently large timescale, shouldn't it?
If, for instance, the average temperature in Portland this January was 45 below, the Columbia froze solid, and we were buried in seven feet of snow, shouldn't it be possible to say "That's not normal!" with some degree of scientific certainty?
Eli: Not sure where you're seeing the conflict between me and the definition you cite. One can always compute the slope and call it a trend. Given, however, the presence of cyclic and irregular contributions, that computation (as I illustrated) will be unreliable. In the case of global mean temperature, we need 20-30 years to define a trend.
Quasarpulse: If things happen that are very far from the climatology of the weather, then, sure. In the case of the Arctic sea ice, the 2007 ice was something like 6 standard deviations away from the mean. In the case of global mean temperatures, we're not looking at such extraordinarily large jumps.
In the vein of extraordinarily large deviations was (a few years ago now) the first thunderstorm on the north slope of Alaska, and the first butterfly. Both were so extraordinary that the Eskimo had no words for them.
You can always compute a slope given two points (otoh if you have every taught you know some students make do with one), however the slope is not a trend. It only becomes a trend if there is a time series with a significant number of points. You have actually shown this
The reason for being picky (and right) is that if you stick with two points being able to define a trend you are going to be run over by the pseudos.
In response to quasarpulse, you wrote:
"In the case of the Arctic sea ice, the 2007 ice was something like 6 standard deviations away from the mean. In the case of global mean temperatures, we're not looking at such extraordinarily large jumps."
I think that is a good example of a tipping point. Temperature a little warmer produced a sudden, non-linear result -- the stunning summer 2007 breakup.
Around tipping points statistical measures (trend, deviation) become useless. Tread carefully, ever mindful of thin ice....
Having pointed a lot of innocents to this thread, I feel it might help to elaborate on Eli's point.
Would it be clearer to say if we have annual temperature numbers, for two years (any two, not necessarily contiguous) we have a change. Because we don't have a series, we don't know what's going on.
If we had daily measurements of temperature, and took two of them, we would have a change, but not a trend. Again we don't know what's going on, without measuring at many intervening points -- how many? Depends, which is the point of your excellent topic.
And by contrast,
If we have, say, the height of an oak sapling for two years, we have a trend; we know that there is an ordered time series -- trees never grow smaller -- although we haven't made a measurement every day or every year.
PS, for early warning, google your own topic title; far more pointers to it are out there than the few I posted, many from blogs I've never heard of. Apres moi, le deluge.
Regarding dko's comment.
Isn't use of "tipping point" a step too far at this juncture?
I thought the major reason for the 2007 losses was put down to wind and sea conditions being favourable for forcing the ice out of the Arctic basin.
Of course, higher temperatures played a part in making the ice thinner and more amenable to being compressed and "transported" by the winds. But I thought that one reason 2008 wasn't another record low year was precisely because the synoptic conditions weren't (as) favourable this last summer as they were in 2007.
P. Lewis
Hank, Eli: I see there's a language issue involved. The distinction we're all drawing is between a number that you can compute (and, Eli, I've seen slopes presented based on zero data points -- young earth creationists and other such people), and a number that means something about the physical system.
I think trying to use change or slope for the merely computable, and trend for the meaningful number runs in to the problem that many of these distinctions do of people forgetting which is which (accuracy vs. precision anyone?), or actively disagreeing about which is which.
What I think I'll do is go for 'meaningful trend', rather than merely trend, for the one that is, and slope or change for the merely computable. The distinction is important. But I'm not sure how to make it clearly without adding words (like meaningful).
dko, anon(P. Lewis) on tipping points.
One of the things I don't like about the term is that, as the comments by the two of you illustrate, it seems to mean rather different things to different people. On the more minimal side, which it looks like dko is taking, I agree that the Arctic ice changes illustrate a tipping point. On the more major side (commitment to systemic global change), I'd agree with P. Lewis that it doesn't.
2007 alone doesn't, I think, show a tipping point. The year was meteorologically unusual in the Arctic, with multiple parts (clouds, temperatures, winds) all aiming towards destroying the ice cover. And it did so with great abandon. The mark of a tipping point is that when other parts of the system return to more normal (as 2008 was in the Arctic melt season), your part of interest does not show the formerly normal response. In 2008, with more or less typical weather, there was not a more or less typical ice minimum. We repeated the wildly unusual minimum of 2007.
As dko suggested, you can't draw your lines through different sides of a tipping point. We have a clear change in summer 2007. Extents at other times of year haven't (yet) shown such a dramatic change. But for August-September, we're now in a new regime.
Hank: Thanks for the positive mentions. I don't see anything novel in the referral logs or google. Google only shows your comments at realclimate, Jules' Klimaatblog, and one other blog. Mostly just looks like people are coming back from holidays.
Still, a different hope I have is to write things that people can use elsewhere.
I will argue with Eli to save 'trend' and 'change' as simple words understood by nonscientists.
Google define:trend
and define:change
Back on topic -- long ago I had found a FTP site somewhere that made available a way for budding new field workers to figure out what statistical value they could get from their work.
Things like -- what will you measure, how often will you measure it, how many different places on your site will you measure it -- and then help deciding whether to choose to detect "up or not" or "down or not" or "up, no change, or down" --- and then told them how many years, or how many site visits, or how many sample observations, they'd have to add to their research plan to have a hope of detecting a change.
I wonder if there's still something like this around. I haven't found one recently.
It was humbling. I'd started a forest fire revegetation by doing a baseline botany survey, and then making some changes on some of the grid squares. The site told me to come back in 200 years to have some clue if anything I'd done would help. This confirmed what the several good biologists I knew told me -- and really emphasized the value of doing a solid baseline and recording it somewhere someone could find it later and be able to use it.
Three notes -- Gavin found the site I was remembering (above), and it's been withdrawn, they'd oversimplified their advice for field workers, apparently.
On the question of how to make sure you have a big enough sample that it doesn't affect the result -- I think this question over at RC is for you; it's so far down in a huge thread on a different subject, you may not see it; it arose from my pointing the fellow here and he's read some of your Trends posts, so http://www.realclimate.org/index.php/archives/2009/05/moncktons-deliberate-manipulation/langswitch_lang/sp#comment-126244
I think he wants to know how you can be sure 30 years is enough, and why won't 100 or 1000 change the result. But I wasn't understanding his questions well, so over to you if you like.
Third loose end -- would you list your several Trends posts in one place with a pointer to the samples you posted on the web for people to practice on? I'm not sure I've found everything and don't know how to best point someone to the whole.
As per discussions at Deltoid, #56-58, let us talk about centered vs backwards trends.
Of course, I agree 100% that centered trends are the most accurate description of what was happening in some year.
Unfortunately, since "data from the future is unavailable at this time", I've found this awkward to explain to people, and sometiems not very effective.
It is unsatisfying to many people to be told: "we really can't say much about what's happening now until 10-15 years from now", especially in competition with those who think 7 years is a definite trend :-) and say so.
But, it seems to me that there is a motivational & pedagological role for backward trends (n addition to centered), as I said at Deltoid:
"Consider the question: at the end of any year in the 20th century, if we do the linear regression from year-29 to year, what would we have thought was happening?"
Especially in looking at history (of science or anything else), people generally resonate to "With the information available at the time, the belief was... or the decision was...", whereas centered/forward is taking advantage of hindsight, and for many people, that just doesn't "feel good".
Among other things, using my Fig 1., since it has the actual years on it, shows it was plausible for people in the 1960s to have been thinking that a clear (but modest) cooling trend had been established.
Hank: I've been running around a lot lately, and will be for another week, so catching up is a challenge. The comment/question you link to is a good one, though, and worth a more direct response than can be had from the notes I've already written. I've put a placeholder comment over at realclimate.
His question, I think, is different from what you think. Namely, I used only 120 (or 150, depends on which climate note) years of data. And, those 120 years are special -- they're the period where for at least part of it, we argue that human activity has affected the climate system in significant ways. So a) do you get the same answers if you use 120 years that are definitely not affected this way, b) do you get the same answers if you use 1000 years to look at the question (maybe from 1500-1620 30 year averaging doesn't have the properties I've demanded). I've at least eyeballed enough graphs of annually-resolved data to be confident myself that the 30ish year period will hold up. But that's my eyeballs. A post with directly relevant illustrations is much better.
Your suggestion of a post which collects links and provides an overview to my assorted notes on trying to figure out what climate is is a good one. I'll be getting to that, perhaps after one more individual post which will look at setting the upper bound on a reasonable climate period.
John:
As a matter of pragmatics, I agree that for the recent period, we're stuck with using trends computed with data ending today rather than centered here. I think we do want to wave a flag that this is something we do with reluctance. If we don't, or can't, use trends centered on the date of interest we're subject to the same mistake as people in the late 1960s to mid 1970s could have made in thinking that they were in a cooling trend. Time centered shows that they weren't. You can't know what the next 15 years will be (though we're working on it of course :-).
I agree that in reading history, you can't blame people for not knowing what was going to happen in the next 15 years. Depending on situation, though, I might be critical of them for not allowing for the fact that they don't know what the next 15 years will look like.
The backward trends, since they're computable all the way to the present day, I agree, have their pedagogical uses. So does, for example, my Simplest climate model. Both just need to be used with caution, which I realize you do.
Yes. My issue is the pedagogy, and good articulations & especially good visualizations of:
a) At any point, what do we know, and how much uncertainty is there?
(both in measurements, and in computed trends).
b) Now that we have more data, what more do we know *was* happening?
The goal is explaining this better to the general audience.
Your trends posts are helpful.
Yes. My issue is the pedagogy, and good articulations & especially good visualizations of:
a) At any point, what do we know, and how much uncertainty is there?
(both in measurements, and in computed trends).
b) Now that we have more data, what more do we know *was* happening?
The goal is explaining this better to the general audience.
Your trends posts are helpful.
Thanks for this.
Two questions:
1) Where is your website with the programs?
2) Do the trend-windows overlap in the analyses for plots 1 & 2, or are they disjoint?
It seems like successive slopes would become more significantly autocorrelated as the trend length window increases, which would also lower the variance of the slopes.
Alternately, if you estimated the slopes over independent chunks of data, you'd have a smaller number of slope observations which might increase your variance estimate. Perhaps that would give guidance on an optimal window length.
Dave:
I've updated the article with the link, and will repeat it here -- http://www.radix.net/~bobg/blogsupport/trend_results.tar
The trend computations are repeated every 12 months. When you're looking at a 25 year period for the trend, it's a long time before you have independent trend estimates. Actually somewhat more than the 25 year period itself -- the weather is autocorrelated, so we need a bit of time to elapse between 25 year spans before they are truly independent.
Optimal, of course, depends on what you want the trend estimates for. My concern here was the simple business of 'how long do you need in order for your trend estimate to not be sensitive to how long a period you chose'. That's clearly in the 20-30 year range.
Bob,
Thanks for the link to the code. I was looking at this for data in a different realm, and coded up something similar in R. I haven't generalized it much, but it looks like a similarly sized window applies to my realm as well.
I tried it with non-overlapping regions, and it didn't see a significant difference, but the trend in my data is fairly stable.
Re. John Mashey's point: Numerically, the backwards looking trend from t=today is the same as the middle-centered trend around t=today-window/2. They are just different names for the same quantity. For any decision made at t=today, you'd have exact same information available no matter which name you give it.
Another perhaps useful example of how this is figured out for a particular data set -- and how it requires first accumulating enough data to have an idea of natural variability, when it's a new instrument:
http://www.biogeosciences.net/7/621/2010/bg-7-621-2010.pdf
"... over ten years of satellite-derived chlorophyll and productivity data have accumulated, can we begin to detect and attribute climate change-driven trends in productivity? Here we compare recent trends in satellite ocean colour data to longer-term time series from three biogeochemical models (GFDL, IPSL and NCAR). We find that detection of climate change-driven trends in the satellite data is confounded by the relatively short time series and large interannual and decadal variability in productivity. Thus, recent observed changes in chlorophyll, primary production and the size of the oligotrophic gyres cannot be unequivocally attributed to the impact of global climate change. Instead, our analyses suggest that a time series of ∼40 years length is needed to distinguish a global warming trend from natural variability. In some regions, notably equatorial regions, detection times are predicted to be shorter (∼20−30 years). Analysis of modelled chlorophyll and primary production from 2001–2100 suggests that, on average, the climate change-driven trend will not be unambiguously separable from decadal variability until ~2055. Because the magnitude of natural variability in chlorophyll and primary production is larger than, or similar to, the global warming trend, a consistent, decades-long data record must be established if the impact of climate change on ocean productivity is to be definitively detected."
Rather belatedly, but as I keep pointing to this thread -- I wonder if you can explain with the same basic approach how taking more instrument observations is also a way to reduce uncertainty or increase precision well beyond the precision available from the individual instrument on one observation?
I'm thinking of the obvious -- temperature weather stations -- but also thinking of another issue, satellite GPS for elevation in looking at glacial rebound and sea level rise -- where I've seen people claim (a "professional surveyor" was cited) that because one instrument making one measurement is is only accurate to plus or minus X, the science can't claim any better precision using multiple instruments in multiple passes.
I'm going from my vague recollection from Stat 101 in the 1970s, thinking about things
like soil loss on a mountainside, taking a few observations over decades was comparable to taking many more observations over a few years, to have a reasonable chance of detecting a trend.
Hank:
Never too late. Science is a long-term discussion. That's why comments are still open.
For once, I might already have addressed one of your questions. The post is aimed at the average, rather than trend, but the basic mathematics involved are the same:
http://moregrumbinescience.blogspot.com/2010/03/how-can-annual-average-temperatures-be.html
A cross-reference:
http://tamino.wordpress.com/2011/07/16/trend-and-noise/
Another cross-reference (there's no convincing people about statistics, as this seems to prove again):
http://www.skepticalscience.com/news.php?p=2&t=58&&n=1025#65219
(Pielke Senior in the comments)
I humbly recommend:
http://bartonpaullevenson.com/30Years.html
and
http://bartonpaullevenson.com/NoWarming15Years.html
Post a Comment